So I'm sitting there in my office at home, coding up Anton's Triangle Tutorial program in an effort to learn OpenGL. While I do this, the COVID-19 virus is busy multiplying in the world and getting a lot of people sick. But since I'm quarantined, I keep myself busy translating Anton's C/C++ code into Java. I'm using Java/Scala for my project because that's where I've spent of the majority of time in my career for the past ten years and I was curious how far I can push the platform.
In Java I started to use the Lightweight Java Game Library (lwjgl) which has a very good OpenGL bindings. Small note that the light library I'm writing on top of lwjgl is written in pure Java, but most of my client code is written in Scala. The lwjgl bindings are good because they take advantage of a few features of the JVM which make it straightforward to work with native libraries.
The first of these features is Java NIO. A few weeks ago I went through Jenkov.com's Java NIO Tutorials since I was a bit rusty on Java NIO. Using Java NIO you can expose native memory to the native OpenGL API's through a safe JVM interface, which is exactly what the native OpenGL library requires.
The second feature was introduced in Java 5 in 2004, static imports. Using Static imports you can simulate Standard C/C++ #include directive, which exposes variables, functions, and classes to your default namespace without any object or static class qualifiers. So, OpenGl code in C++ like this:
while(!glfwWindowShouldClose(window)) {
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glUseProgram(shader_prog);
glBindVertexArray(vao);
glDrawArrays(GL_TRIANGLES, 0, 3);
glfwPollEvents();
glfwSwapBuffers(window);
}
Looks like this in Java. Yes, they are identical.
while(!glfwWindowShouldClose(window)) {
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT)
glUseProgram(shader_prog);
glBindVertexArray(vao);
glDrawArrays(GL_TRIANGLES, 0, 3);
glfwPollEvents();
glfwSwapBuffers(window);
}
Not all of the code is identical, however. Instead of this block of C++:
float points[] = {
0.0f, 0.5f, 0.0f,
0.5f, -0.5f, 0.0f,
-0.5f, -0.5f, 0.0f
};
GLuint vbo = 0;
glGenBuffers(1, &vbo);
glBindBuffer(GL_ARRAY_BUFFER, vbo);
glBufferData(GL_ARRAY_BUFFER, 9 * sizeof(float), points, GL_STATIC_DRAW);Your Java code will look like this (assuming you have a similar definition for points:
# Scala
private val points = Array(
0.0f, 0.75f, 0.0f,
0.75f, -0.75f, 0.0f,
-0.75f, -0.75f, 0.0f)
# Java
int vbo = glGenBuffers();
glBindBuffer(GL_ARRAY_BUFFER, vbo);
Buffer buffer = BufferUtils.createFloatBuffer(data.length).put(data);
glBufferData(GL_ARRAY_BUFFER, (FloatBuffer)buffer.flip(), GL_STATIC_DRAW);The program generates a color triangle and uses a mouse uniform to place a highlight over the cursor. Click on the image below to see the image in its full fidelity.
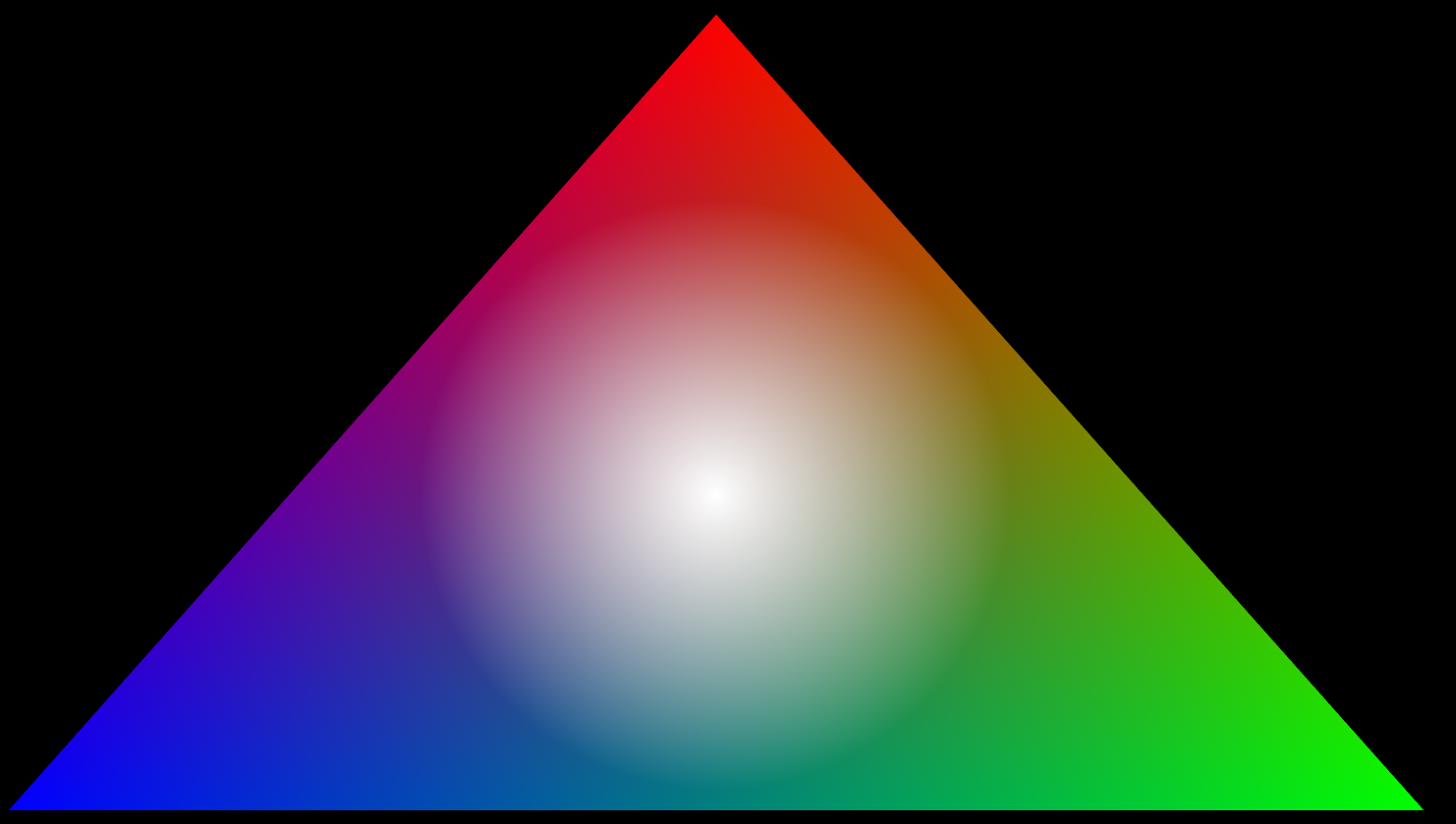
The fall off is linear with the percentage of white being a linear fall off from 1->0 proportional with the distance from the mouse cursor over 300 pixels. The shader code looks like this:
#version 400
const float PI_2 = 1.57079632679489661923;
uniform vec2 u_resolution;
uniform vec2 u_mouse;
in vec3 color;
out vec4 frag_color;
#define FALLOFF (u_resolution.x / 16.0)
void main() {
float distMouse = min(FALLOFF, distance(gl_FragCoord.xy, u_mouse));
float lin_falloff = 1.0-(min(distMouse, FALLOFF) / FALLOFF);
vec3 finalColor = mix(color, vec3(1.0,1.0,1.0), lin_falloff);
frag_color = vec4(finalColor, 1.0);
}In mathematical terms, it looks like this (generated from GNU Octave):
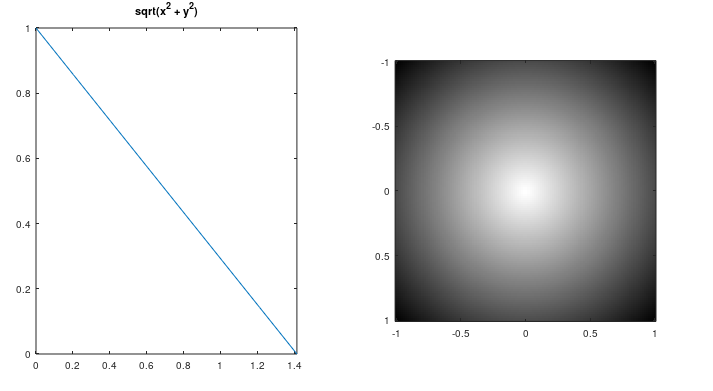
Which didn't look so bad in Octave, but in the original triangle image above the edge was too harsh and I wanted to soften it. I tried to square the falloff, yielding this curve:
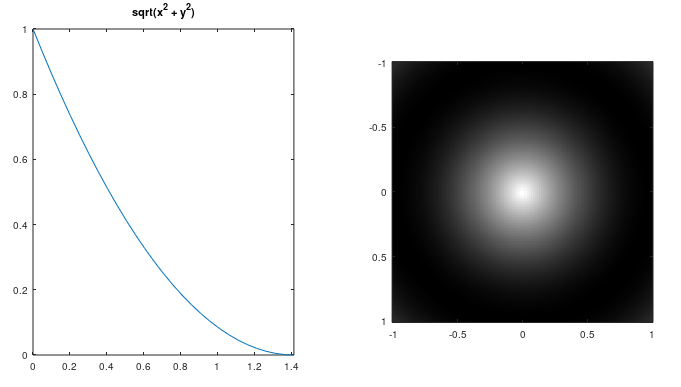
But I felt the falloff dropped too abruptly. I decided to try cos(x). Notice how the center bulge is brighter:
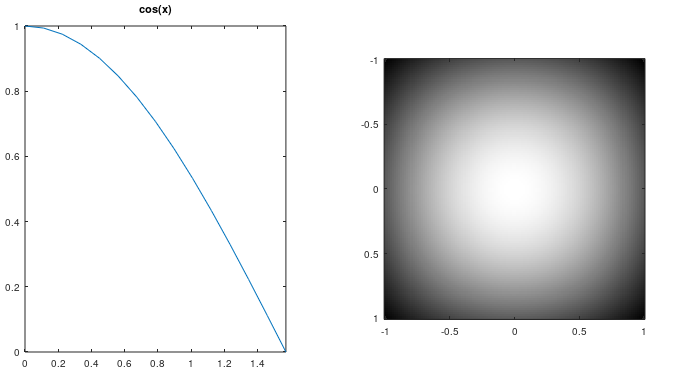
Yet when viewed in OpenGL, the edge was still too abrupt, maybe even moreso!
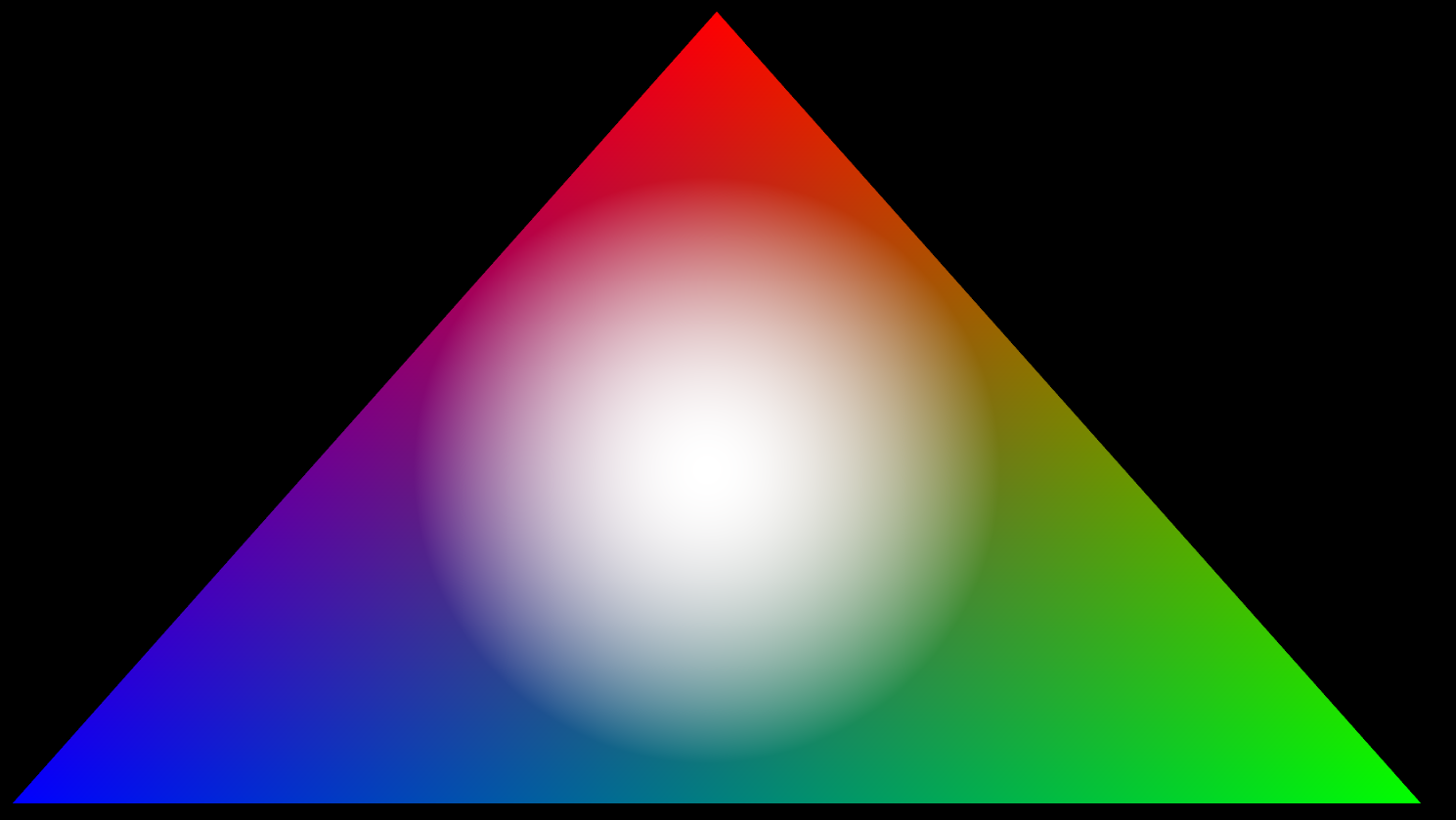
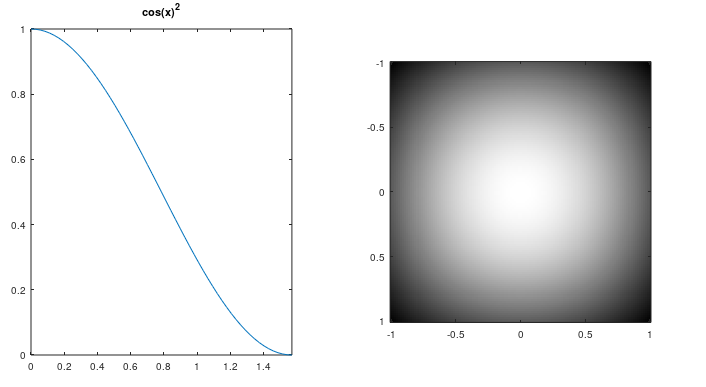
So I decided to square cos(x) and notice t he beautiful S-curve I was looking for!
So I decided to generate a bunch of curves and try them all out:
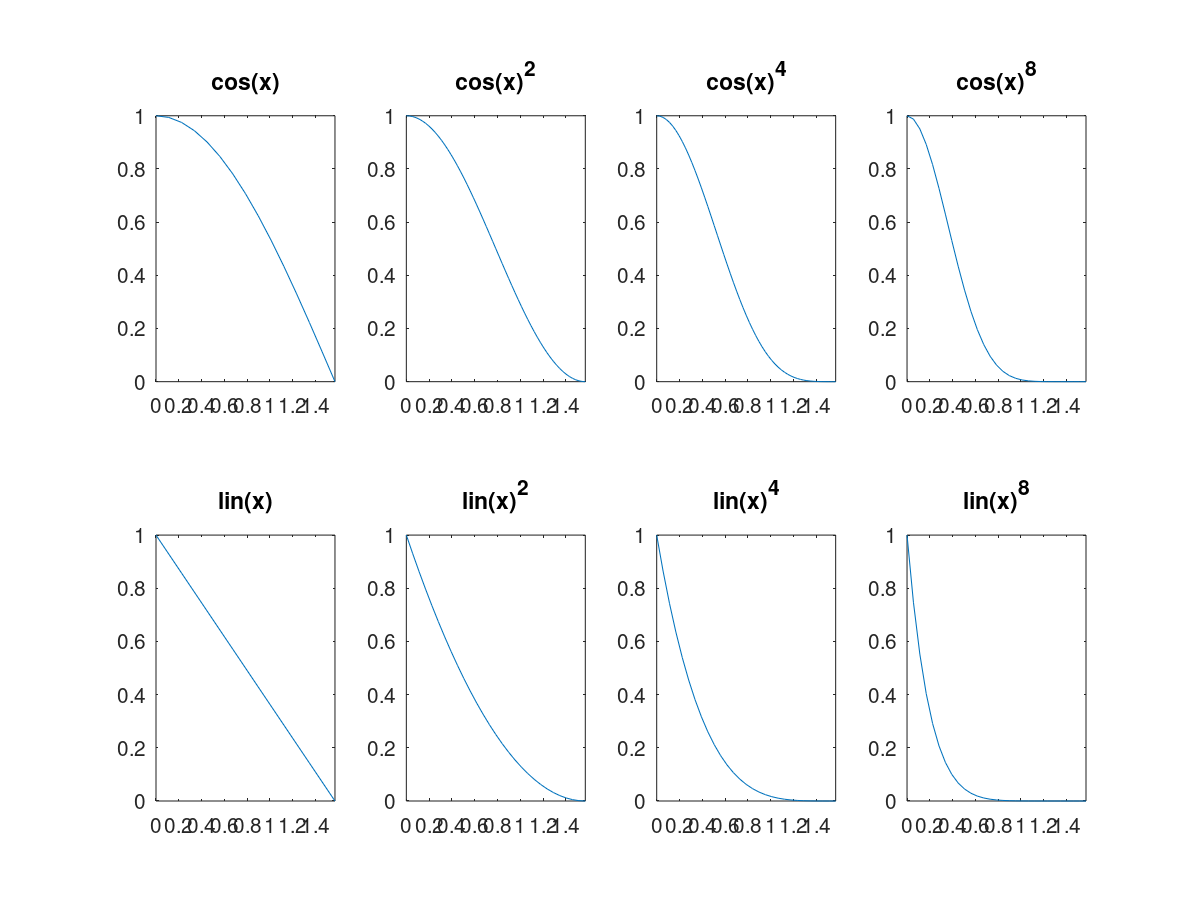
In the end, none of the linear falloff variants pleased me and I went with cos(x)^2
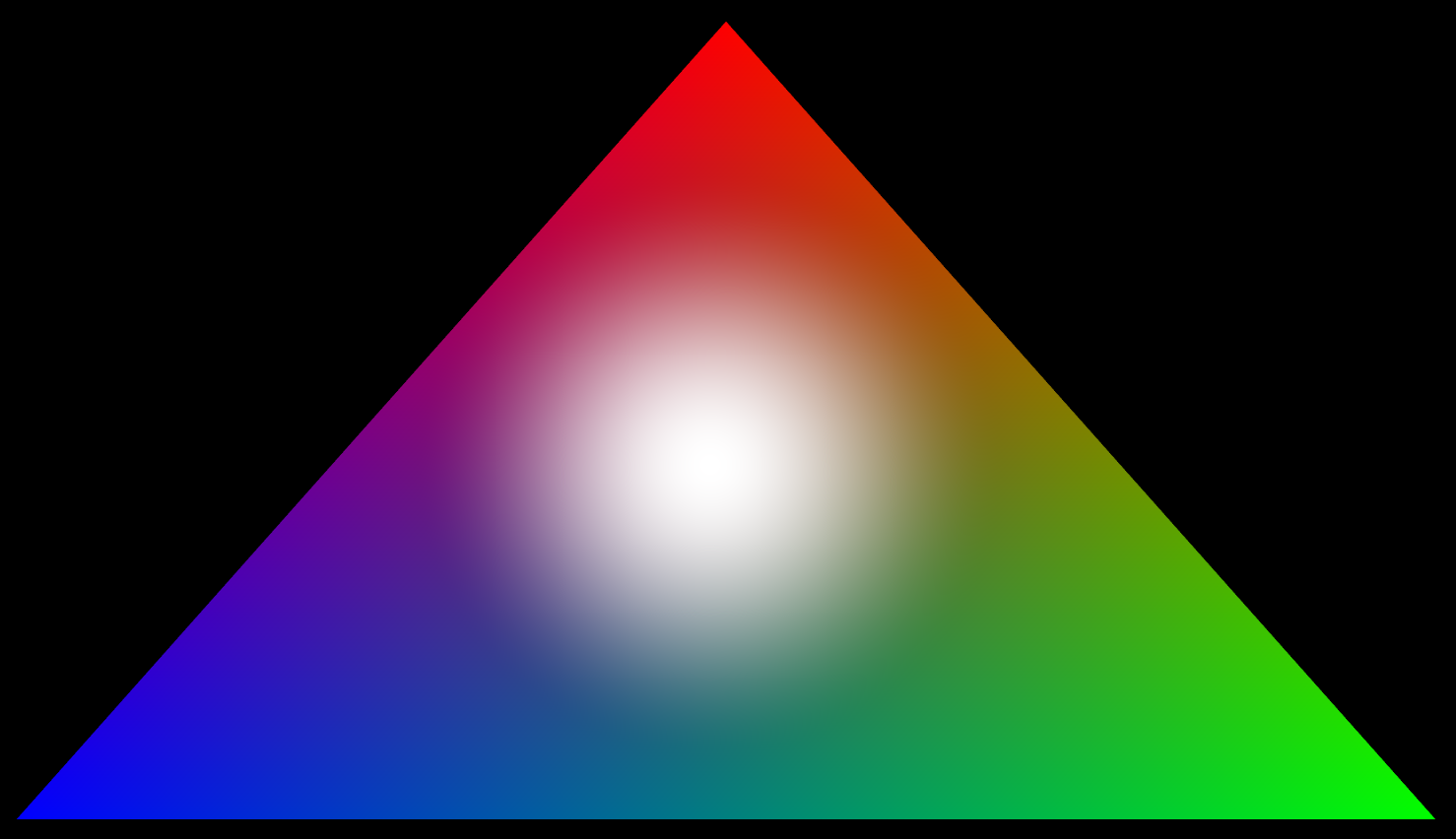
This gave me the best central bulge and a smooth gradient that faded away without any noticeable edge. QED!